waca's field

# 2차원 배열 (TWO-DIMENSIONAL ARRAYS) 2차원 배열은 사실 일차원 배열이다. 단지, 배열의 요소가 1차원 배열로 이루어져 있을 뿐이다. 2차원 배열을 선언할 때 우리는 주로 int arr[3][5] 와 같이 선언한다. 하지만 우리는 실제로 길이가 3인 배열 x를 생성했을 뿐이고, x의 각 요소들이 길이가 5인 일차원 배열일 뿐이다. 아래 그림을 살펴보자. 이 그림은 2차원 배열의 메모리 구조를 보여주고 있다. 먼저, 회색으로 통째로 칠해진 블럭을 보면 3개의 포인터를 가질 수 있는 크기로 되어 있다. 그리고 그 포인터를 따라가면, 5개의 integer 변수를 포함할 수 있는 녹색블럭이 각 3개가 나온다. C 에서 arr[i][j] 를 찾아가는 과정은 이렇다. 첫째로, x[i] 포인터..

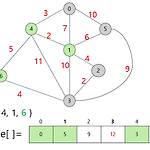
# 최단 경로 최단 경로(shortest path)문제는 정점 u와 정점 v를 연결하는 경로 중 간선들의 가중치 합이 최소가 되는 경로를 찾는 문제다. 간선의 가중치는 경우에 따라 비용, 거리, 시간 등으로 해석될 수 있다. 아래의 그래프를 살펴보자. 정점 0에서 정점 3으로 가는 최단 경로는 ( 0, 4, 1, 2, 3 )이고 이 때의 비용(거리)은 3 + 2 + 4 + 2 = 11 이다. 정점 0에서 정점 3으로 가는 다른 경로가 얼마든지 존재하지만, 최소의 거리로 갈 수 있는 방법은 이 방법 뿐이다. 가중치는 가중치 인접 행렬이라고 불리는 2차원 배열에 저장된다. 가중치 인접 행렬은 기존의 인접행렬과 차이점이 있다. 기존의 인접 행렬에서는 간선이 없는 구간에는 행렬의 값을 0으로 했었다. 그러나 가..

# 멱집합 구하는 문제 문제) S가 n개의 원소로 된 집합일 때 S의 멱집합(powerset)은 모든 가능한 S의 부분집합이다. 즉, S = { a, b, c }이면 powerset(S) = { { }, { a }, { b }, { c }, { a, b }, { a, c }, { b, c }, { a, b, c } } 이다. powerset(S)를 구하는 순환 함수를 작성하라. # 풀이 비트 연산을 이용하는 문제다. 순환으로 구현해야 하는 만큼 순환별 규칙을 생각할 필요가 있었고, 값을 하나 증가시키는 걸 그 규칙으로 삼았다. 하나의 순환 안에서의 반복문이 비트연산의 핵심인데, 처음엔 이해가 어려워도 하나하나 손으로 써가면서 확인하면 그 규칙이 눈에 들어올 것이다. /********************..

# 히프의 개념 히프(heap)는 "더미"라는 뜻이다. 히프는 여러 개의 값들 중에서 가장 큰 값이나 가장 작은 값을 빠르게 찾아내도록 만들어진 자료구조이다. 히프는 간단히 말하면 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰 (작은) 이진 트리를 말한다. 즉 A가 B의 부모 노드라고 하고 부모 노드의 키 값이 자식 노드의 키 값보다 항상 크다고 하면, 다음과 같은 조건이 항상 성립하는 트리이다.$Key(A) >= Key(B)$ 히프는 완전 이진 트리(complete binary tree) 이며 중복된 값을 허용함에 유의한다. 이진 탐색 트리에서는 중복된 값을 허용하지 않았다. 히프 안에서 데이터들은 느슨한 정렬 상태를 유지한다. 즉, 큰 값이 상위 레벨이고 작은 값이 하위 레벨에 있다는 정도의 ..

# Kruskal의 MST 알고리즘 Kruskal의 알고리즘은 탐욕적인 방법(greedy method)을 이용한다. 탐욕적인 방법은 알고리즘 설계에 있어 중요한 기법 중 하나다. 결정을 해야 할 때, 그 순간에 가장 좋다고 생각되는 것을 해답으로 선택하는 방법을 말한다. 순간 순간의 최선을 선택해 최종적인 해답에 도달하는 과정인 것이다. 당시에 최적이라고 생각했던 선택들을 모은다고 해서 최종적인 결과가 최적의 해답이라는 보장은 없다. 따라서 탐욕적인 방법은 항상 검증이 필요하다. 다행히 Kruskal 알고리즘은 최적의 해답을 주는 것으로 증명되어 있다. Kruskal의 알고리즘은 최소 비용 신장 트리가 최소 비용의 간선으로 구성됨과 동시에 사이클을 포함하지 않는다는 조건을 기초로 각 단계에서 사이클을 이..

# Prim의 MST 알고리즘 최소 비용 신장 트리(MST: minimum spanning tree)는 신장 트리 중에서 사용된 간선들의 가중치 합이 최소인 신장트리를 말한다. 최소 비용 신장 트리를 이용하면, 도로 건설이나 전기 회로설계, 통신 인프라 구축 등의 문제를 가장 효율적으로 처리할 수 있게 된다. Prim의 알고리즘은 시작 정점에서부터 출발하여 신장 트리 집합을 단계적으로 확장해나가는 방법을 사용한다. 시작 단계에서는 시작 정점만이 신장 트리 집합에 포함된다. Prim은 앞 단계에서 만들어진 신장 트리 집합에 인접한 정점들 중에서 최소 간선으로 연결된 정점을 선택하여 트리를 확장한다. 이 과정은 트리가 n - 1개의 간선을 가질 때까지 계속된다. // n개의 정점을 가지는 신장 트리의 간선은..

# 비둘기집 원칙 문제 문제) 비둘기집 원칙이란 함수 f가 n개의 상이한 입력에 대해 n개보다 작은 상이한 출력이 나온다면 $a\neq$ $b$ 이고 $f(a) = f(b)$인 두 개의 입력 a, b가 존재한다는 것이다. 이와 같이 입력값이 상이하면서 함수값이 같은 a,b를 찾는 C프로그램을 작성하라. # 풀이 이 문제는 한 가지 함수를 미리 정해두고 프로그램을 작성한다. 그 후 함수 내에 같은 y값이 나오는 x값들이 있는지 확인하는 프로그램을 작성하면 된다. /************************************************* ** 비둘기집 원칙 프로그램 *************************************************/ #include #include //..

# Horner의 법칙 문제 //horner의 법칙 관련 개념 설명은 맨 밑에 있습니다. 문제) Horner의 법칙은 주어진 점 $x0$ 에서 최소의 곱으로 다항식 $A(x) = a_nx^n+a_{n-1}x^{n-1}+\ldots+a^1x+a_0$ 를 계산하는 것으로 이 법칙은$A(x_0) = ( ... ((a_nx_0 + a_{n-1})x_0 + ... + a_1)x_0 + a_0)$ 이다. Horner의 법칙을 사용하여 다항식을 계산하는 C프로그램을 작성하라. # 풀이 Horner의 법칙 문제를 풀 때는 직접 손으로 먼저 계산하며 그 과정을 이해해야 한다. 곱셈으로 도출된 값이 다음 덧셈에 이용되고 또 그렇게 도출된 나머지가 곱셈되어 다음 덧셈에 이용되는 그 과정을 이해해야 한다. /*********..

퀴즈에 등장하는 개념 요약 // 해당 도서를 읽지 않으시는 분들도 생각하고 풀어보실 수 있습니다.# 전진 이동법 전진 이동법(Move to front method)은 어느 항목이 한 번 탐색되고 나면, 그 항목을 데이터 집합의 가장 앞(링크드 리스트에서는 헤드)에 위치시키는 방법이다. 이렇게 하면 한 번 찾은 항목을 연이어 또 찾는 경우 단번에 탐색을 완료할 수 있다. MS 워드의 '최근 문서'기능과 같은 원리로 동작한다고 생각하면 이해가 쉽다. 전진이동법의 한계는 한 번 탐색된 항목이 곧 이어 또다시 검색될 가능성이 높은 데이터 집합에서만 사용해야한다 점이다. # 전위법 전위법(Transpose method)은 탐색된 항목을 바로 이전 항목과 교환한다는 것 말고는 기본적으로 전진 이동법과 같은 전략을 ..

이것만은 알고 갑시다. 문제) 더블 링크드 리스트는 탐색이 느린 대신, 데이터 요소의 삽입 / 삭제가 빠른 자료구조다. 배열을 위해 구현되었던 Insertion_Sort( )함수가 더블 링크드 리스트를 정렬할 수 있게 구현하라. 풀이 한 가지 확실한 건 이 문제는 머릿 속으로만 해결할 수 없는 문제다. 반드시 일어날 수 있는 상황을 상정하고 직접 손으로 그림을 그려가며 풀어야 한다. 논리가 그렇게 간단하지 않다. 아래 적혀 있는 풀이 소스는 가독성을 위해 이중연결리스트(더블링크드리스트) 구조체와 삽입정렬 알고리즘만이 적혀 있다. 이미 완성되어 있는 이중연결리스트의 첫 번째 노드의 주소, 즉 헤드가 매개변수로 전달되었다 생각하고 밑의 코드를 살펴보도록 하자. 전체 소스는 최하단에 첨부해 두었으니 잘 작동하..